文字
背景
行間

2018年6月の記事一覧
閑話 黄金比 その3
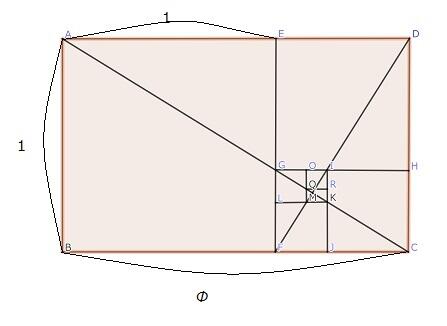
 縦横の辺の長さの比が黄金比になっている長方形を黄金長方形と呼びます。左上図で言えば、AB:BC=1 : Φ
縦横の辺の長さの比が黄金比になっている長方形を黄金長方形と呼びます。左上図で言えば、AB:BC=1 : Φ ここで、この長方形から正方形を切り出すと残った長方形も黄金長方形になります。
左上図でいえば、長方形ABCDから、正方形ABFEを切り取った残りの長方形DEFCが黄金長方形です。
もとの長方形ABCDの辺の長さと小さな長方形DEFCの辺の長さを比べると $$\frac{1}{\phi}$$ 倍となります。ここで、また長方形DEFCから正方形DEGHを切り取った残りの長方形CHGFもまた黄金長方形となり、辺の長さは $$\frac{1}{\phi}$$ 倍となります。この操作を無限に続けていくとどんどん小さな黄金長方形ができ、そのたびに辺の長さは $$\frac{1}{\phi}$$ 倍となります。
左上図のように任意に選んだ元の長方形とそれから正方形を切り取って残った長方形のそれぞれの対角線を引くとどれも同じ一点で交わります。無限に小さくなる長方形は、この点に収束していくわけです。
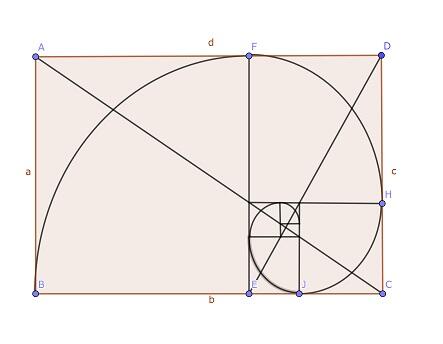
左下図は、正方形部分に4分の1円を描いて作ったらせんです。きれいですね。
問1 黄金長方形を作図してみよう。
問2 黄金比 その2で示した連分数と今回の黄金長方形の分割を考察してみよう。

