文字
背景
行間

校長花ごよみ
第45回鍋山祭 書道パフォーマンス



 本日11:00に行われた書道パフォーマンス。本校の中庭で多くのギャラリーの見守る中、書道部の書道ガールズが、気持ちを一つに、詩のことばに心をこめて一気に書き上げました。素晴らしいの一言です。
本日11:00に行われた書道パフォーマンス。本校の中庭で多くのギャラリーの見守る中、書道部の書道ガールズが、気持ちを一つに、詩のことばに心をこめて一気に書き上げました。素晴らしいの一言です。昨日、今日と連日PTAの広報委員会の皆様がこのパフォーマンスも含め鍋山祭を取材していただいています。本当にありがとうございます。PTA広報が楽しみです。
第45回鍋山祭 第2日

 本日は、鍋山祭の第2日目です。本日の発表は一般公開となっております。
本日は、鍋山祭の第2日目です。本日の発表は一般公開となっております。鍋山祭確認クイズ 1.参加団体は、いくつでしょう。 2.演劇鑑賞の整理券の配布場所・時間は。 3.各調理等食品提供団体のメニューは。 4.各部・同好会の特別企画の開始時間は。5.PTAバザーの場所は。
鍋山祭心に刻もうクイズ 1.あなたのお気に入りの団体は。(投票がありますので、お願いします) 2.装飾が美しかった、工夫されてた団体は。3.鍋山祭一番の思い出は。
(右の写真は、私のお気に入りの工芸部の藍染ハンカチと美術部の缶バッチです。)
ご来場の際は、お気をつけてお越し下さい。お待ちしてます。
第45回鍋山祭 第1日



 いよいよ、文化委員会を中心に全生徒、職員で準備してきた今年度の鍋山祭が始まりました。各クラスや委員会、部活動・同好会の発表はどこも熱が入っていてすばらしいものとなっています。部活動展示のほんの一端をご紹介いたします。
いよいよ、文化委員会を中心に全生徒、職員で準備してきた今年度の鍋山祭が始まりました。各クラスや委員会、部活動・同好会の発表はどこも熱が入っていてすばらしいものとなっています。部活動展示のほんの一端をご紹介いたします。工芸部の藍染作品(手拭いやコースターなど)や陶芸作品の展示・販売、彫金や鋳造作品の展示、写真部の作品展示とカレンダー等の販売、華道部の生け花展示。なお、生け花の水盤は、工芸部の生徒の作品となっています。美術部では、作品展示と缶バッチの展示・販売をしています。ご来場の際は、ぜひともご覧いただき感想をいただけると幸いです。また、生物部では、佐倉高校の豊かな樹木に着目し来校者がそれらを鑑賞できるよう発表がされていました。
明日は、通常の会場での展示発表に加えて部活動毎に特別企画が目白押しです。
なお、ご来場者には、文化委員会で丹精を込めて作成した見やすい鍋山祭のパンフレットがありますので御見学の際の参考としていただけると幸いです。
The summer solstice 2018










今日は、二十四節気の第10番目の夏至です。佐倉市では、日の出の時間が4:24、日の入りが18:59です。佐倉市の緯度では昼の時間と夜の時間との比は、約1.6です。本日は、一年でもっとも日が長くなる日ですので佐倉高校にとって鍋山祭の準備日として最適な1日といえるのではないでしょうか。昨日の午後から校内は鍋山祭の会場へと装いを一変すべく槌音?が鳴り響いています。
生徒たちは、鍋山祭に向けて、熱い思いとともに多くの時間と労力をかけて準備してきましたが、いよいよその全貌を現す時が近づいてきました。6月23日(土)は、一般公開日ですのでお楽しみにしてください。
話は代わりますが、昨日は、第100回全国高等学校野球選手権記念東千葉・西千葉大会の試合の組み合わせ(千葉県高等学校野球連盟HPへ)が発表になりました。本校野球部は西千葉大会に出場します。本校の初戦は四街道北高校で、大会日程が順調に進めば、7月13日の青葉の森公園球場で行われる第1試合(試合開始は9時)となります。皆さんの熱い応援をよろしくお願いします。
閑話 黄金比 その1
先日、参加した千葉県高等学校教育研究会数学部会の春季研究大会の講演で、講師の先生が和算の問題を現在使える公式を使わずに解くとしたらというお話しのなかで「黄金比」を使って解くというものがあり、そういえば「黄金比」自体とっても興味深いものであることを思い出し、今回はその一端に触れてみたい。
黄金比は、エウクレイデス(ユークリッド)が「原論」で明快な定義を与えている。そこでは線分を単純に分けて得られる線分の長さの比で次のように定義し「外中比」(黄金比のこと)と呼んでいる。
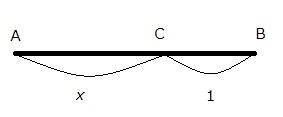 「線分全体と長い切片との比が、長い切片と短い切片との比になる場合、線分は外中比に切り分けられたという。」左図でいえば、
「線分全体と長い切片との比が、長い切片と短い切片との比になる場合、線分は外中比に切り分けられたという。」左図でいえば、
 が成り立っているということ。つまり、短い切片CBの長さを基準にして、$$AB=x,CB=1$$ とおくと $$\frac{x+1}{x}=\frac{x}{1}$$ が成り立つ。よって、両辺に$$x$$を掛けて整理すると、$$x^2-x-1=0$$ ・・・① が得られる。
が成り立っているということ。つまり、短い切片CBの長さを基準にして、$$AB=x,CB=1$$ とおくと $$\frac{x+1}{x}=\frac{x}{1}$$ が成り立つ。よって、両辺に$$x$$を掛けて整理すると、$$x^2-x-1=0$$ ・・・① が得られる。
問2 問1で求めた正の解をΦ(ファイ)とする。Φの値はどのくらいだろう。
黄金比は、エウクレイデス(ユークリッド)が「原論」で明快な定義を与えている。そこでは線分を単純に分けて得られる線分の長さの比で次のように定義し「外中比」(黄金比のこと)と呼んでいる。
 「線分全体と長い切片との比が、長い切片と短い切片との比になる場合、線分は外中比に切り分けられたという。」左図でいえば、
「線分全体と長い切片との比が、長い切片と短い切片との比になる場合、線分は外中比に切り分けられたという。」左図でいえば、問1 $$x$$の2次方程式①を解いてみよう。
問2 問1で求めた正の解をΦ(ファイ)とする。Φの値はどのくらいだろう。
関数電卓等で近似値を確かめてみよう。
問3 問2でΦの近似値を関数電卓等でΦ2 や $$\frac{1}{\phi}$$ の近似値を確かめてみよう。
何か、気づいたことはありますか。
問4 ΦとΦ2 、 $$\frac{1}{\phi}$$ との関係を考えてみよう。
問5 下の数式の値はいくつでしょう。
$$\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots } } } }$$
以上、興味をもった生徒は校長室まで話に来てください。
次回は 黄金比の連分数表現について
$$1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\cdots}$$
問3 問2でΦの近似値を関数電卓等でΦ2 や $$\frac{1}{\phi}$$ の近似値を確かめてみよう。
何か、気づいたことはありますか。
問4 ΦとΦ2 、 $$\frac{1}{\phi}$$ との関係を考えてみよう。
問5 下の数式の値はいくつでしょう。
$$\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots } } } }$$
以上、興味をもった生徒は校長室まで話に来てください。
次回は 黄金比の連分数表現について
$$1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\cdots}$$

