2018年6月の記事一覧

閑話　黄金比　その２

投稿日時 : 2018/06/23  sakura-h  カテゴリ:閑話

$$x=1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\cdots}$$　と置くと

 $$x=1+\frac{1}{x}$$ とかける。

問１　$$x$$ はどんな値でしょう。
問２　Φ を黄金比とします。　$${\phi}^{n}$$ を　$${\phi}^{n-1}$$ と $${\phi}^{n-2}$$  で表わしてください。

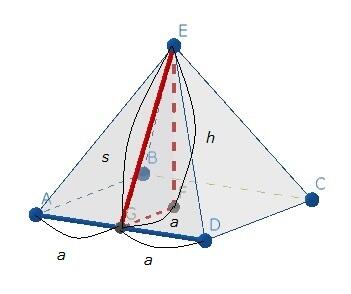pyramid古代エジプト人は Φ を知っていた？pyramidとΦのロマン

ピラミッドが左図のように、底面の１辺の長さが 2a の正方形の四角錐で、各側面の三角形の面積がピラミッドの高さ h を一辺とする正方形の面積に等しくなっていたとします。このとき、各側面の三角形の高さを s として、次の問を考えてください。

問３　\frac{s}{a}　は、どんな値でしょう。