文字
背景
行間
2018年7月の記事一覧
SSH特別講義
sakura-h
SGHにおいては、昨日、今日と日本政策金融公庫から２名の講師が来てくださり、２年生がビジネスプランの研究の進め方など班ごとにアドバイスをいただいていました。また、SSHにおいては、KEK（高エネルギー加速器研究機構）から本校の卒業生である宍戸寿郎先生にお越しいただきました。先生は、最新宇宙論に触れられ、宇宙の成り立ちに関して、宇宙誕生直後に同じ数だけあったはずの粒子と反粒子が、現在の宇宙ではどうして、粒子ばかり存在するのかという現代物理学の謎に挑むため「CP対称性の破れ」（粒子と反粒子の性質の違い）に関する実験（電子と陽電子を衝突させる）やこの実験を行うための加速器や測定装置についてお話しいただきました。講義の最後には、生徒たちに「どの分野に進んでも、その分野に貢献できるような人になってほしい」と激励の言葉をいただきました。宍戸先生ありがとうございました。 閑話 その７ 黄金比
ある人が階段を登ろうとしています。その人は、１歩で登れるのは、最高で２段までとします。つまり、階段を１歩では１段か２段で登れるとします。いま階段が、ｎ段としたら、登り方は何通り（Fｎ）あるか考えてみましょう。
１段しかない階段なら登り方は１通り (1) しかないので F1＝１
２段だと、１段目から１段で登る方法 (1)+1 か、最初から一気に２段で登る (2) かの２通りとなるので F2＝２
３段だと、２段目から１段で登る方法 ((1)+1)+1、(2)+1 と１段目から２段で登る方法 (1)+2 の３通りあるので、F3＝３
４段だと、３段目から１段で登る方法 (((1)+1)+1)+1、((2)+1)+1、((1)+2)+1 と２段目から２段で登る方法 ((1)+1)+2、(2)+2の５通りなので、F4＝５
５段だと、4段目から１段で登る方法 ((((1)+1)+1)+1)+1、(((2)+1)+1)+1、(((1)+2)+1)+1、(((1+1))+2)+1、((2)+2)+1と３段目から２段で登る方法 (((1)+1)+1)+2、((2)+1)+2、((1)+2)+2 の８通りあるので、F5＝８ となります。
こうして、可能な登り方の数列 { Fn } は、{１，２，３，５，８、・・・}
となります。
ｎ段の階段の登り方を考えてできた数列の第３項以降の各項 Fn は、その１段前までの登り方 Fn-1 とさらにその１段前までの登り方 Fn-2 との和として表すことができます。
つまり、数列 { Fn } は、F1＝１、F2＝２、 Fn＝ Fn-1 ＋ Fn-2 （ｎ≧３）で
帰納的に定義される数列となります。
問１ ここで違う問題を考えてみましょう。ある男が、うさぎの番（つがい）を１対、壁で囲まれた場所に放しました。ウサギの番については、毎月新しい番を生み、生まれた番も次の月から番を生むとします。そしてウサギは死なないとすると１年間に何対のウサギが生まれるでしょうか。
問２ ここで数列 { Fn }を次のようにつくります。まず、F1、F2 を好きな数に決めます。その２つの数で和を作り3番目の数 F3 とします。更に、2番目と3番目の数の和を作り４番目の数 F4 とします。この操作を繰り返して20番目くらいまでできたら数列の比
を計算してみてください。$$\lim_{n\to \infty}\frac{F_n}{F_{n-1 } }$$ はどんな値に近づくでしょう。
１段しかない階段なら登り方は１通り (1) しかないので F1＝１
２段だと、１段目から１段で登る方法 (1)+1 か、最初から一気に２段で登る (2) かの２通りとなるので F2＝２
３段だと、２段目から１段で登る方法 ((1)+1)+1、(2)+1 と１段目から２段で登る方法 (1)+2 の３通りあるので、F3＝３
４段だと、３段目から１段で登る方法 (((1)+1)+1)+1、((2)+1)+1、((1)+2)+1 と２段目から２段で登る方法 ((1)+1)+2、(2)+2の５通りなので、F4＝５
５段だと、4段目から１段で登る方法 ((((1)+1)+1)+1)+1、(((2)+1)+1)+1、(((1)+2)+1)+1、(((1+1))+2)+1、((2)+2)+1と３段目から２段で登る方法 (((1)+1)+1)+2、((2)+1)+2、((1)+2)+2 の８通りあるので、F5＝８ となります。
こうして、可能な登り方の数列 { Fn } は、{１，２，３，５，８、・・・}
となります。
ｎ段の階段の登り方を考えてできた数列の第３項以降の各項 Fn は、その１段前までの登り方 Fn-1 とさらにその１段前までの登り方 Fn-2 との和として表すことができます。
つまり、数列 { Fn } は、F1＝１、F2＝２、 Fn＝ Fn-1 ＋ Fn-2 （ｎ≧３）で
帰納的に定義される数列となります。
問１ ここで違う問題を考えてみましょう。ある男が、うさぎの番（つがい）を１対、壁で囲まれた場所に放しました。ウサギの番については、毎月新しい番を生み、生まれた番も次の月から番を生むとします。そしてウサギは死なないとすると１年間に何対のウサギが生まれるでしょうか。問２ ここで数列 { Fn }を次のようにつくります。まず、F1、F2 を好きな数に決めます。その２つの数で和を作り3番目の数 F3 とします。更に、2番目と3番目の数の和を作り４番目の数 F4 とします。この操作を繰り返して20番目くらいまでできたら数列の比
短時間豪雨
昨日7月9日の14:30からSSHの運営指導委員会が地域交流施設において行われました。その会議が終わるころから雨が降り出し、30分間くらいでしたが雷とともにものすごい雨が降りました。マレーシア、タイ、シンガポールなど東南アジアの国々のスコールのように、道路だったところが、あっという間に川に代わるような、まさにバケツで撒いたような強さと量の雨でした。この雨で恩恵を受けたとすれば東郷池の水が増えていつになく水がきれいになったことです。普段は泳いでいる姿をはっきり・くっきりとみることができない東郷池の鯉や鮒たちの姿を今日はしっかりととらえることができました。
野球応援練習
本日、13:30から気持ちのこもった野球応援の練習が応援委員会と吹奏楽部、野球部員を中心に行われました。ここに参加してくれた生徒の諸君は、ここ一か月、文化祭の準備、自分の部活動、第２回定期考査の準備等あるなか、頑張る友人のために、応援練習を続けてきてくれました。そんな心温かい生徒諸君を見るにつけ、校長として誇りに思います。予定どおり試合が行われれば、７月１３日の青葉の森公園野球場の第１試合が本校野球部の初戦です。是非とも皆様、応援のほどよろしくお願いします。 SGH特別授業
1年生は
SGHの課題研究のテーマを決めていくうえで、今後解決してみたいテーマをどのように一つに絞っていくのかが重要になります。本日は、ビジネスプラン作成を参考にして、体験的に学ぶ講座を、日本政策金融公庫 南関東創業支援センター所長でいらっしゃる寺田博史様を講師としてお招きして講義をお願いしました。考える対象を絞って、よいアイデアの出すための方法や、テーマを絞りこむための視点の置き方など
これからの探究活動を進めるうえでとても大切なことを学ぶことができたと思います。暑い中、講師をお引き受けいただいた寺田先生、本当にありがとうございました。
SGHの課題研究のテーマを決めていくうえで、今後解決してみたいテーマをどのように一つに絞っていくのかが重要になります。本日は、ビジネスプラン作成を参考にして、体験的に学ぶ講座を、日本政策金融公庫 南関東創業支援センター所長でいらっしゃる寺田博史様を講師としてお招きして講義をお願いしました。考える対象を絞って、よいアイデアの出すための方法や、テーマを絞りこむための視点の置き方などこれからの探究活動を進めるうえでとても大切なことを学ぶことができたと思います。暑い中、講師をお引き受けいただいた寺田先生、本当にありがとうございました。
夢 新舞台
今日7月8日（日）は、第73回国民体育大会関東ブロック大会が、茨城県神栖市にできた新カヌー会場で開催されました。この会場は、来年茨城県で開催される「いきいき茨城ゆめ国体2019」のカヌー会場となるところです。イメージキャラクターの「いばラッキー」が開会式に参加してくれました。今日の大会は、各都県を勝ち抜いてきた代表者だけが参加する大会ですのでどの競技も質の高いすばらしいものでした。多少風は強かったもののまずまずのコンディションで競技が行われてよかったです。参加した選手の諸君は得るものが多かったのではないでしょうか。今後に向けてステップアップのいい機会になったと思います。
千葉県で震度５弱
本日は、本来なら七夕の話題なのでしょうが、皆さんご存知の通り、７日午後８時２３分ごろ、関東地方で強い地震が発生しました。気象庁によると、千葉県北東部で震度５弱が観測されたそうです。震源地は千葉県東方沖。震源の深さ66㎞で、マグニチュードは6.0と推定されています。この地震による津波の心配はないということでした。私はその時間千葉市にいて、携帯電話に一斉に地震を告げる緊急地震速報が鳴り響いた矢先に結構な揺れを感じました。皆さんの地域は大丈夫でしたか。被災されてないことを祈ります。
その後、JR千葉駅に着いても、電車が安全点検のため各駅に停まっていて、動き始めても結局、家に帰れたのが22時過ぎとなり通常より1時間30分ほど帰宅にかかる時間が多くなりました。西日本・中部地方で過去になかったほどの大雨による災害が起こっており、天災に対する備えの重要さをあらためて実感したところです。
その後、JR千葉駅に着いても、電車が安全点検のため各駅に停まっていて、動き始めても結局、家に帰れたのが22時過ぎとなり通常より1時間30分ほど帰宅にかかる時間が多くなりました。西日本・中部地方で過去になかったほどの大雨による災害が起こっており、天災に対する備えの重要さをあらためて実感したところです。
閑話 その６ 黄金比
さて、そろそろ Φ について慣れてきた？ところですが、ここでちょっと復習しておきましょう。
Φ は、2次方程式 $${\phi}^2-{\phi}-1=0$$ の正の解となりますので
$${\phi}=\frac{1+\sqrt{5 } }{2}$$ でした。そして、もう一つの負の解を Φ´ とすると、
$${\phi}^{\prime}=\frac{1-\sqrt{5 } }{2}$$ ですからこれを Φ で表すと、$${\phi}'=-\frac{1}{\phi}$$ ・・・（ア）となります。
問１ （ア）の関係を確かめてください。
問２ Φ と Φ’ の積と和を求めてください。
Φ に１を足すと２乗になったり、１を引くと逆数になったり
Φ っておもしろくないですか。
「閑話 その2」 の問２の問題ですが、
$${\phi}^2={\phi}+1$$ の両辺に Φ を掛けると $${\phi}^3={\phi}^2+{\phi}$$
この操作を続けていくと $${\phi}^{n}={\phi}^{n-1}+{\phi}^{n-2}$$ となります。
つまり、Φ の任意のべき乗は、その前のべき乗とさらに一つ前のべき乗を足せばいいことがわかります。
ここで、初項１、公比 Φ の数列 $$\lbrace{1,\phi,\phi^2,\phi^3,\phi^4, \phi^5,\cdots}\rbrace$$ を考えます。
いままで見てきたことから、Φ のべき乗を、Φ の１次の項だけで書き換えることができます。
実際に計算してみると $${\phi}^2={\phi}+1$$ ですから、
$${\phi}^3={\phi}^2+{\phi}={(}{\phi}+1{)}+{\phi}=2{\phi}+1$$
$${\phi}^4={\phi}^3+{\phi}^2={(}2{\phi}+1{)}+{(}{\phi}+1{)}=3{\phi}+2$$
$${\phi}^5={\phi}^4+{\phi}^3={(}3{\phi}+2{)}+{(}2{\phi}+1{)}=5{\phi}+3$$
$${\phi}^6={\phi}^5+{\phi}^4={(}5{\phi}+3{)}+{(}3{\phi}+2{)}=8{\phi}+5$$
したがって、もとの数列は、$$\lbrace{1,\phi,\phi+1,2\phi+1,3\phi+2, 5\phi+3,8\phi+5,\cdots}\rbrace$$ となります。
ここで Φ の係数に着目すると、｛１，１，２，３，５，８、・・・・｝
となります。この数列どこかで見たことありませんか。理系の人にはおなじみですよね。これについては次回また。
Φ は、2次方程式 $${\phi}^2-{\phi}-1=0$$ の正の解となりますので
$${\phi}=\frac{1+\sqrt{5 } }{2}$$ でした。そして、もう一つの負の解を Φ´ とすると、
$${\phi}^{\prime}=\frac{1-\sqrt{5 } }{2}$$ ですからこれを Φ で表すと、$${\phi}'=-\frac{1}{\phi}$$ ・・・（ア）となります。
問１ （ア）の関係を確かめてください。
問２ Φ と Φ’ の積と和を求めてください。
Φ に１を足すと２乗になったり、１を引くと逆数になったり
Φ っておもしろくないですか。
「閑話 その2」 の問２の問題ですが、
$${\phi}^2={\phi}+1$$ の両辺に Φ を掛けると $${\phi}^3={\phi}^2+{\phi}$$
この操作を続けていくと $${\phi}^{n}={\phi}^{n-1}+{\phi}^{n-2}$$ となります。
つまり、Φ の任意のべき乗は、その前のべき乗とさらに一つ前のべき乗を足せばいいことがわかります。
ここで、初項１、公比 Φ の数列 $$\lbrace{1,\phi,\phi^2,\phi^3,\phi^4, \phi^5,\cdots}\rbrace$$ を考えます。
いままで見てきたことから、Φ のべき乗を、Φ の１次の項だけで書き換えることができます。
実際に計算してみると $${\phi}^2={\phi}+1$$ ですから、
$${\phi}^3={\phi}^2+{\phi}={(}{\phi}+1{)}+{\phi}=2{\phi}+1$$
$${\phi}^4={\phi}^3+{\phi}^2={(}2{\phi}+1{)}+{(}{\phi}+1{)}=3{\phi}+2$$
$${\phi}^5={\phi}^4+{\phi}^3={(}3{\phi}+2{)}+{(}2{\phi}+1{)}=5{\phi}+3$$
$${\phi}^6={\phi}^5+{\phi}^4={(}5{\phi}+3{)}+{(}3{\phi}+2{)}=8{\phi}+5$$
したがって、もとの数列は、$$\lbrace{1,\phi,\phi+1,2\phi+1,3\phi+2, 5\phi+3,8\phi+5,\cdots}\rbrace$$ となります。
ここで Φ の係数に着目すると、｛１，１，２，３，５，８、・・・・｝
となります。この数列どこかで見たことありませんか。理系の人にはおなじみですよね。これについては次回また。
生徒会役員選挙
今日は、生徒会役員選挙が行われます。今回の選挙は第71代の生徒会執行部役員を選ぶ大切な選挙となります。今回は、生徒会長については競争選挙となっています。また、他の役職（副会長、書記、会計）については信任投票となります。会長選挙についてそれぞれの候補が、昼休みを使って選挙活動を行ってきました。今日は投票前に立候補者全員の立会演説会が行われました。特に両会長候補とも、しっかりと有権者の生徒全員に考えと思いを伝えられたと思います。また、生徒の皆さんは、競争選挙、信任投票のいずれにしても代表を選ぶわけですから立候補者の考えや思いをしっかりと聞いて投票をして欲しいと思います。 閑話 黄金比 その５
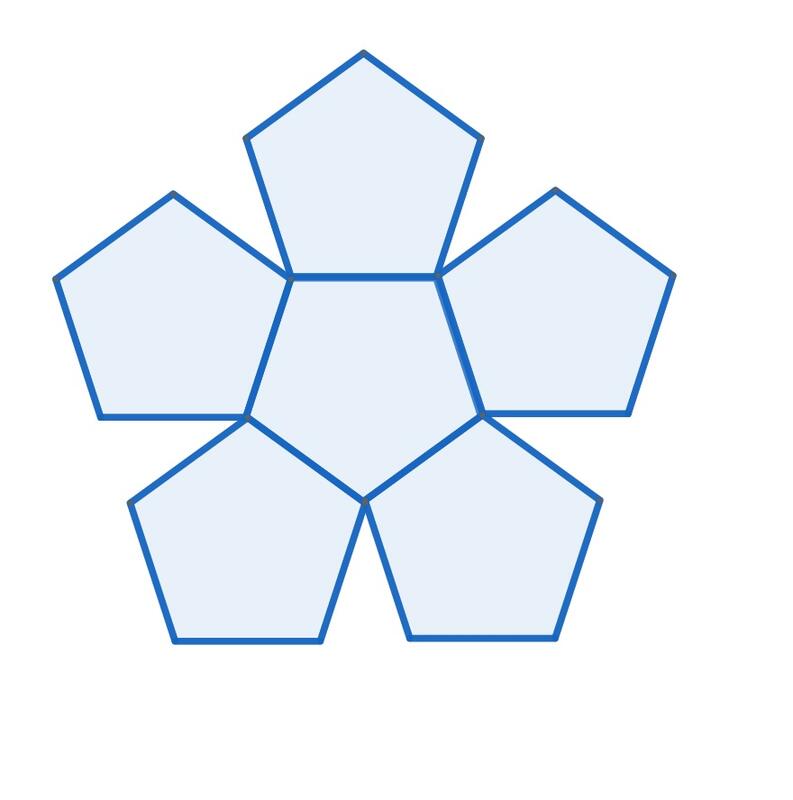
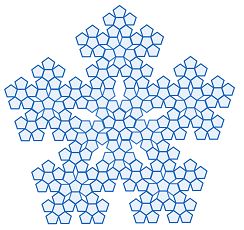
正五角形によるフラクタルその４でお話しした正五角形を使った美しい図形についてのお話です。正五角形を６枚使って「黄金三角形」（底辺に対する横の辺の比が Φ の二等辺三角形）の切込みが入ったひとまわり大きな正五角形（左の図形）を作ります。この正五角形をまた６組集めてさらに大きな正五角形を作りこれをさらに６組集めて都合正五角形216個で作った図形が真ん中の図形です。右の図形は、真ん中の図形をさらに６組集めて作った図形です。この操作はどこまでも続けられます。単純な構成方法を繰り返すしているだけなのに、こんなに美しい図形ができるのは驚きです。