文字
背景
行間

校長花ごよみ
夢 新舞台



 今日7月8日(日)は、第73回国民体育大会関東ブロック大会が、茨城県神栖市にできた新カヌー会場で開催されました。この会場は、来年茨城県で開催される「いきいき茨城ゆめ国体2019」のカヌー会場となるところです。イメージキャラクターの「いばラッキー」が開会式に参加してくれました。
今日7月8日(日)は、第73回国民体育大会関東ブロック大会が、茨城県神栖市にできた新カヌー会場で開催されました。この会場は、来年茨城県で開催される「いきいき茨城ゆめ国体2019」のカヌー会場となるところです。イメージキャラクターの「いばラッキー」が開会式に参加してくれました。今日の大会は、各都県を勝ち抜いてきた代表者だけが参加する大会ですのでどの競技も質の高いすばらしいものでした。多少風は強かったもののまずまずのコンディションで競技が行われてよかったです。参加した選手の諸君は得るものが多かったのではないでしょうか。今後に向けてステップアップのいい機会になったと思います。
千葉県で震度5弱
本日は、本来なら七夕の話題なのでしょうが、皆さんご存知の通り、7日午後8時23分ごろ、関東地方で強い地震が発生しました。気象庁によると、千葉県北東部で震度5弱が観測されたそうです。震源地は千葉県東方沖。震源の深さ66㎞で、マグニチュードは6.0と推定されています。この地震による津波の心配はないということでした。私はその時間千葉市にいて、携帯電話に一斉に地震を告げる緊急地震速報が鳴り響いた矢先に結構な揺れを感じました。皆さんの地域は大丈夫でしたか。被災されてないことを祈ります。
その後、JR千葉駅に着いても、電車が安全点検のため各駅に停まっていて、動き始めても結局、家に帰れたのが22時過ぎとなり通常より1時間30分ほど帰宅にかかる時間が多くなりました。西日本・中部地方で過去になかったほどの大雨による災害が起こっており、天災に対する備えの重要さをあらためて実感したところです。
その後、JR千葉駅に着いても、電車が安全点検のため各駅に停まっていて、動き始めても結局、家に帰れたのが22時過ぎとなり通常より1時間30分ほど帰宅にかかる時間が多くなりました。西日本・中部地方で過去になかったほどの大雨による災害が起こっており、天災に対する備えの重要さをあらためて実感したところです。
閑話 その6 黄金比
さて、そろそろ Φ について慣れてきた?ところですが、ここでちょっと復習しておきましょう。
Φ は、2次方程式 $${\phi}^2-{\phi}-1=0$$ の正の解となりますので
$${\phi}=\frac{1+\sqrt{5 } }{2}$$ でした。そして、もう一つの負の解を Φ´ とすると、
$${\phi}^{\prime}=\frac{1-\sqrt{5 } }{2}$$ ですからこれを Φ で表すと、$${\phi}'=-\frac{1}{\phi}$$ ・・・(ア)となります。
問1 (ア)の関係を確かめてください。
問2 Φ と Φ’ の積と和を求めてください。
Φ に1を足すと2乗になったり、1を引くと逆数になったり
Φ っておもしろくないですか。
「閑話 その2」 の問2の問題ですが、
$${\phi}^2={\phi}+1$$ の両辺に Φ を掛けると $${\phi}^3={\phi}^2+{\phi}$$
この操作を続けていくと $${\phi}^{n}={\phi}^{n-1}+{\phi}^{n-2}$$ となります。
つまり、Φ の任意のべき乗は、その前のべき乗とさらに一つ前のべき乗を足せばいいことがわかります。
ここで、初項1、公比 Φ の数列 $$\lbrace{1,\phi,\phi^2,\phi^3,\phi^4, \phi^5,\cdots}\rbrace$$ を考えます。
いままで見てきたことから、Φ のべき乗を、Φ の1次の項だけで書き換えることができます。
実際に計算してみると $${\phi}^2={\phi}+1$$ ですから、
$${\phi}^3={\phi}^2+{\phi}={(}{\phi}+1{)}+{\phi}=2{\phi}+1$$
$${\phi}^4={\phi}^3+{\phi}^2={(}2{\phi}+1{)}+{(}{\phi}+1{)}=3{\phi}+2$$
$${\phi}^5={\phi}^4+{\phi}^3={(}3{\phi}+2{)}+{(}2{\phi}+1{)}=5{\phi}+3$$
$${\phi}^6={\phi}^5+{\phi}^4={(}5{\phi}+3{)}+{(}3{\phi}+2{)}=8{\phi}+5$$
したがって、もとの数列は、$$\lbrace{1,\phi,\phi+1,2\phi+1,3\phi+2, 5\phi+3,8\phi+5,\cdots}\rbrace$$ となります。
ここで Φ の係数に着目すると、{1,1,2,3,5,8、・・・・}
となります。この数列どこかで見たことありませんか。理系の人にはおなじみですよね。これについては次回また。
Φ は、2次方程式 $${\phi}^2-{\phi}-1=0$$ の正の解となりますので
$${\phi}=\frac{1+\sqrt{5 } }{2}$$ でした。そして、もう一つの負の解を Φ´ とすると、
$${\phi}^{\prime}=\frac{1-\sqrt{5 } }{2}$$ ですからこれを Φ で表すと、$${\phi}'=-\frac{1}{\phi}$$ ・・・(ア)となります。
問1 (ア)の関係を確かめてください。
問2 Φ と Φ’ の積と和を求めてください。
Φ に1を足すと2乗になったり、1を引くと逆数になったり
Φ っておもしろくないですか。
「閑話 その2」 の問2の問題ですが、
$${\phi}^2={\phi}+1$$ の両辺に Φ を掛けると $${\phi}^3={\phi}^2+{\phi}$$
この操作を続けていくと $${\phi}^{n}={\phi}^{n-1}+{\phi}^{n-2}$$ となります。
つまり、Φ の任意のべき乗は、その前のべき乗とさらに一つ前のべき乗を足せばいいことがわかります。
ここで、初項1、公比 Φ の数列 $$\lbrace{1,\phi,\phi^2,\phi^3,\phi^4, \phi^5,\cdots}\rbrace$$ を考えます。
いままで見てきたことから、Φ のべき乗を、Φ の1次の項だけで書き換えることができます。
実際に計算してみると $${\phi}^2={\phi}+1$$ ですから、
$${\phi}^3={\phi}^2+{\phi}={(}{\phi}+1{)}+{\phi}=2{\phi}+1$$
$${\phi}^4={\phi}^3+{\phi}^2={(}2{\phi}+1{)}+{(}{\phi}+1{)}=3{\phi}+2$$
$${\phi}^5={\phi}^4+{\phi}^3={(}3{\phi}+2{)}+{(}2{\phi}+1{)}=5{\phi}+3$$
$${\phi}^6={\phi}^5+{\phi}^4={(}5{\phi}+3{)}+{(}3{\phi}+2{)}=8{\phi}+5$$
したがって、もとの数列は、$$\lbrace{1,\phi,\phi+1,2\phi+1,3\phi+2, 5\phi+3,8\phi+5,\cdots}\rbrace$$ となります。
ここで Φ の係数に着目すると、{1,1,2,3,5,8、・・・・}
となります。この数列どこかで見たことありませんか。理系の人にはおなじみですよね。これについては次回また。
生徒会役員選挙
 今日は、生徒会役員選挙が行われます。今回の選挙は第71代の生徒会執行部役員を選ぶ大切な選挙となります。今回は、生徒会長については競争選挙となっています。また、他の役職(副会長、書記、会計)については信任投票となります。会長選挙についてそれぞれの候補が、昼休みを使って選挙活動を行ってきました。今日は投票前に立候補者全員の立会演説会が行われました。特に両会長候補とも、しっかりと有権者の生徒全員に考えと思いを伝えられたと思います。また、生徒の皆さんは、競争選挙、信任投票のいずれにしても代表を選ぶわけですから立候補者の考えや思いをしっかりと聞いて投票をして欲しいと思います。
今日は、生徒会役員選挙が行われます。今回の選挙は第71代の生徒会執行部役員を選ぶ大切な選挙となります。今回は、生徒会長については競争選挙となっています。また、他の役職(副会長、書記、会計)については信任投票となります。会長選挙についてそれぞれの候補が、昼休みを使って選挙活動を行ってきました。今日は投票前に立候補者全員の立会演説会が行われました。特に両会長候補とも、しっかりと有権者の生徒全員に考えと思いを伝えられたと思います。また、生徒の皆さんは、競争選挙、信任投票のいずれにしても代表を選ぶわけですから立候補者の考えや思いをしっかりと聞いて投票をして欲しいと思います。 閑話 黄金比 その5
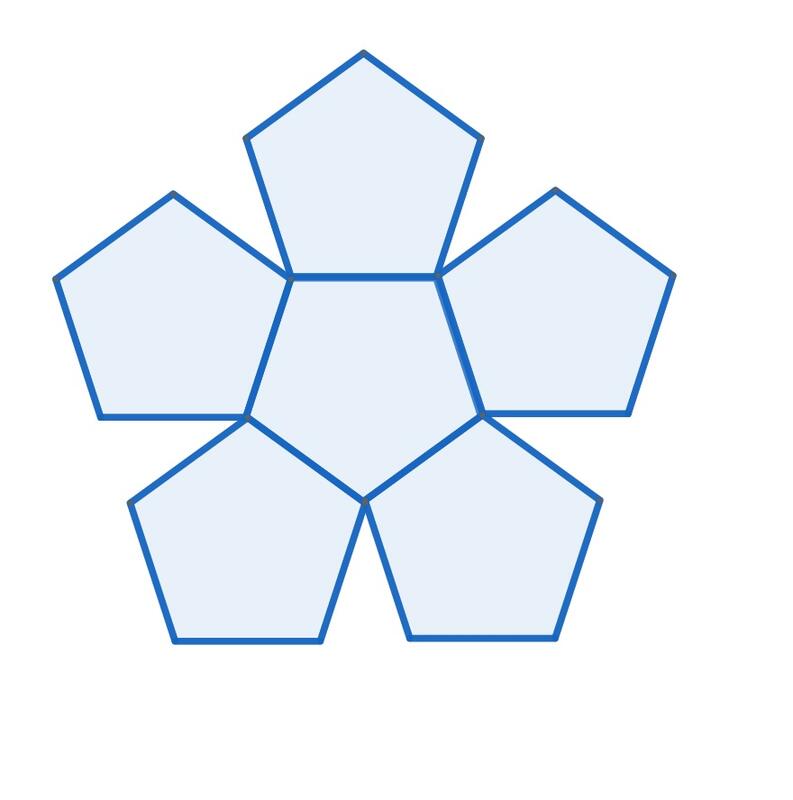
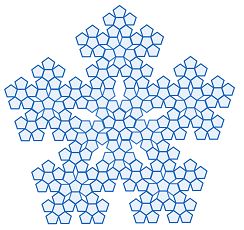
 正五角形によるフラクタル
正五角形によるフラクタルその4でお話しした正五角形を使った美しい図形についてのお話です。正五角形を6枚使って「黄金三角形」(底辺に対する横の辺の比が Φ の二等辺三角形)の切込みが入ったひとまわり大きな正五角形(左の図形)を作ります。この正五角形をまた6組集めてさらに大きな正五角形を作りこれをさらに6組集めて都合正五角形216個で作った図形が真ん中の図形です。右の図形は、真ん中の図形をさらに6組集めて作った図形です。この操作はどこまでも続けられます。単純な構成方法を繰り返すしているだけなのに、こんなに美しい図形ができるのは驚きです。
閑話 黄金比 その4
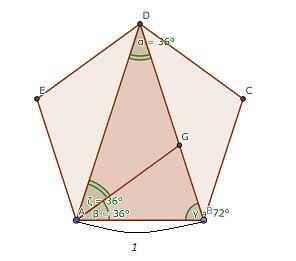 今回は、「正五角形をコンパスと定規で作図してみよう。」ということでヒントととなる?お話をします。
今回は、「正五角形をコンパスと定規で作図してみよう。」ということでヒントととなる?お話をします。左図は、1辺の長さが1の正五角形ABCDEです。△DABは正五角形ABCDEの対角線を2辺とする二等辺三角形です。頂角が 36° 、両底角は、72° となります。(なぜこうなるかは各自で確かめてください)
今、∠DAB の角の二等分線と辺DB との交点を G とします。
問1 点G は正五角形ABCDEの対角線DBをどのような比に分ける点でしょうか。
問2 正五角形ABCDEの対角線の長さはいくつになるでしょう。
問3 与えられた一片の長さをもとに正五角形をコンパスと定規を使って作図するには何が作れればよいでしょうか。それをどのように利用すればよいでしょうか。
問4 与えられた一片の長さをもとに正五角形をコンパスと定規を使って作図してみてください。
関東甲信地方梅雨明け(びっくり)

 本日6月29日、気象庁は関東甲信地方が梅雨明けしたとみられると発表しました。(平成30年の梅雨入りと梅雨明け(速報値))統計を取り始めて以来、関東甲信地方が6月に梅雨明けするのは初めてのことだそうです。これまで関東甲信地方で最も早く梅雨が明けたのは2001年の7月1日だったそうです。
本日6月29日、気象庁は関東甲信地方が梅雨明けしたとみられると発表しました。(平成30年の梅雨入りと梅雨明け(速報値))統計を取り始めて以来、関東甲信地方が6月に梅雨明けするのは初めてのことだそうです。これまで関東甲信地方で最も早く梅雨が明けたのは2001年の7月1日だったそうです。梅雨明けの時期ですが、平年と比べると(7月21日ごろ)より22日早く、昨年と比べても(7月6日ごろ)より7日早い梅雨明けだそうです。
梅雨の期間ですが、今年は梅雨入りしたのが6月6日ですから梅雨明け前日の6月28日までの日数は23日間となります。これは、梅雨の期間が6月11日から7月4日までだった1978年に並んで1番の短さだそうです。(梅雨入り・明けの時期は、秋に再検討され、見直されることもあるそうです)
いずれにしても、このところ一気に真夏に入ってしまったような暑さになっていたので、へんだなぁと思っていましたが、まさか、もう梅雨が明けてしまうなんて本当にびっくりです。熱中症対策(校長室もこのところ連日30℃です)や恵みの雨が少なかったことによる水不足対策にしっかり取り組まないといけないですね。
いずれにしても、このところ一気に真夏に入ってしまったような暑さになっていたので、へんだなぁと思っていましたが、まさか、もう梅雨が明けてしまうなんて本当にびっくりです。熱中症対策(校長室もこのところ連日30℃です)や恵みの雨が少なかったことによる水不足対策にしっかり取り組まないといけないですね。
閑話 黄金比 その3
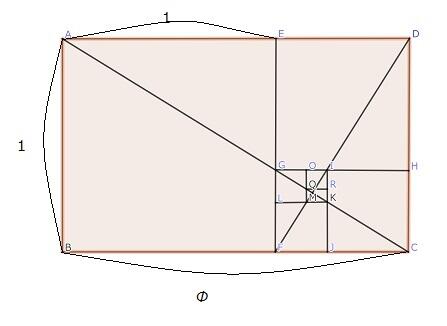
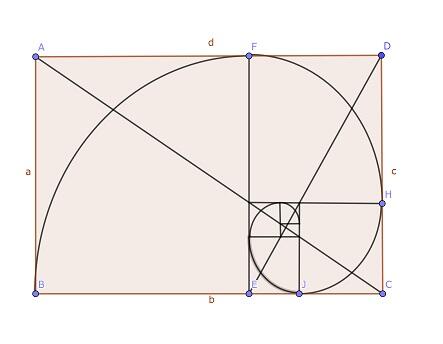 縦横の辺の長さの比が黄金比になっている長方形を黄金長方形と呼びます。左上図で言えば、AB:BC=1 : Φ
縦横の辺の長さの比が黄金比になっている長方形を黄金長方形と呼びます。左上図で言えば、AB:BC=1 : Φ ここで、この長方形から正方形を切り出すと残った長方形も黄金長方形になります。
左上図でいえば、長方形ABCDから、正方形ABFEを切り取った残りの長方形DEFCが黄金長方形です。
もとの長方形ABCDの辺の長さと小さな長方形DEFCの辺の長さを比べると $$\frac{1}{\phi}$$ 倍となります。ここで、また長方形DEFCから正方形DEGHを切り取った残りの長方形CHGFもまた黄金長方形となり、辺の長さは $$\frac{1}{\phi}$$ 倍となります。この操作を無限に続けていくとどんどん小さな黄金長方形ができ、そのたびに辺の長さは $$\frac{1}{\phi}$$ 倍となります。
左上図のように任意に選んだ元の長方形とそれから正方形を切り取って残った長方形のそれぞれの対角線を引くとどれも同じ一点で交わります。無限に小さくなる長方形は、この点に収束していくわけです。
左下図は、正方形部分に4分の1円を描いて作ったらせんです。きれいですね。
問1 黄金長方形を作図してみよう。
問2 黄金比 その2で示した連分数と今回の黄金長方形の分割を考察してみよう。
はやぶさ2がRyuguへ
地球から約3億キロ(地球と太陽の距離の2倍)離れた小惑星Ryugu(リュウグウ)を目指して2014年12月に打ち上げられた小惑星探査機「はやぶさ2」が、いよいよ本日、リュウグウに到着すると国立研究開発法人宇宙航空研究開発機構(JAXA)から発表されました。
また、「はやぶさ2」が24日にリュウグウから約40キロに近づいたときに撮影した画像にはそろばん玉のような形をしたリュウグウとその表面の岩の塊やクレーターが鮮明に確認できるものが公開されています。(JAXAはやぶさ2プロジェクト)
JAXAでは、「はやぶさ2」のリュウグウの高度20㎞地点への到着に際して、本日16時00分~17時00分(予定)に記者会見を開催するそうです。これまで3年半の長旅を緻密な軌道決定と軌道計算に支えられ幾度かの軌道修正を経て飛んできた「はやぶさ2」の今回の小惑星サンプルリターンのミッションには、惑星の起源だけでなく地球の海の水の起源や生命の原材料をも探求するミッションが含まれているということで、多くの謎の解明に向けてこれから行われる数々のミッションの成功がとても楽しみです。
また、「はやぶさ2」が24日にリュウグウから約40キロに近づいたときに撮影した画像にはそろばん玉のような形をしたリュウグウとその表面の岩の塊やクレーターが鮮明に確認できるものが公開されています。(JAXAはやぶさ2プロジェクト)
JAXAでは、「はやぶさ2」のリュウグウの高度20㎞地点への到着に際して、本日16時00分~17時00分(予定)に記者会見を開催するそうです。これまで3年半の長旅を緻密な軌道決定と軌道計算に支えられ幾度かの軌道修正を経て飛んできた「はやぶさ2」の今回の小惑星サンプルリターンのミッションには、惑星の起源だけでなく地球の海の水の起源や生命の原材料をも探求するミッションが含まれているということで、多くの謎の解明に向けてこれから行われる数々のミッションの成功がとても楽しみです。
閑話 黄金比 その2
$$x=1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\cdots}$$ と置くと
$$x=1+\frac{1}{x}$$ とかける。
問1 $$x$$ はどんな値でしょう。
問2 Φ を黄金比とします。 $${\phi}^{n}$$ を $${\phi}^{n-1}$$ と $${\phi}^{n-2}$$ で表わしてください。
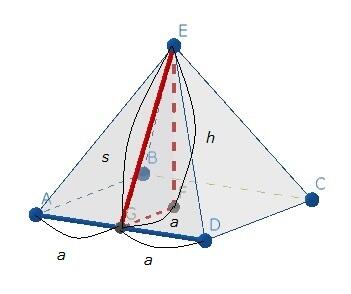 古代エジプト人は Φ を知っていた?pyramidとΦのロマン
古代エジプト人は Φ を知っていた?pyramidとΦのロマンピラミッドが左図のように、底面の1辺の長さが 2a の正方形の四角錐で、各側面の三角形の面積がピラミッドの高さ h を一辺とする正方形の面積に等しくなっていたとします。このとき、各側面の三角形の高さを s として、次の問を考えてください。
問3

